Problema 1
¿A cuántos m/s equivale la velocidad de un avión que se desplaza a 216 km/h?
Solución
| 216 km/h | ||
| = | 216 | Donde 1km = 1 000 m |
| = | 216 000 m/h | Se cancelan los km |
| = | 216 000 | Donde 1h = 3 600 s |
| = | 60 m/s | Se cancelan las h y realizamos la división |
La respuesta la equivalencia, nos queda que 216 km/h = 60 m/s
Problema 2
Un automóvil Porsche de Carrera GT viaja en línea recta con una velocidad media de 1 300 cm/s durante 8 s, y luego con velocidad media de 480 cm/s durante 10 s, siendo ambas velocidades del mismo sentido:
|  |
a) ¿cuál es el desplazamiento total en el viaje de 18 s del automóvil Porsche?.
b) ¿cuál es la velocidad media del automóvil Porsche en su viaje completo?.
Solución
Datos:
Momento 1
|
Momento 2
|
|---|---|
| v1 = 1 300 cm/s | v2 = 480 cm/s |
| t1 = 8 s | t2 = 10 s |
a. El desplazamiento que el automóvil Posche hace en el mismo sentido, es:
Como la formula que utilizaremos es x = v.t
Momento 1
|
Momento 2
|
|---|---|
| x1 = (v1).(t1) | x2 = (v2).(t2) |
| x1 = (1 300 cm/s). (8 s) | x2 = (480 cm/s).(10 s) |
| x1 = 10 400 cm | x2 = 4 800 cm |
El desplazamiento total es:
Xt = X1 + x2
Xt = 10 400 cm + 4 800 cm
Xt = 15 200 cm = 152 m
Xt = X1 + x2
Xt = 10 400 cm + 4 800 cm
Xt = 15 200 cm = 152 m
Entonces el desplazamiento total a los 18 s del Porsche es: 15 200 cm = 152 m
b. La velocidad media del viaje completo del Porsche
Como el tiempo total es:
tt = t1 + t2 = 8 s + 10 s = 18 s
Con el desplazamiento total recién calculado aplicamos:
Δv = xtotal / ttotal
Δv = 152 m / 18 s
Δ v = 8.44 m/s
tt = t1 + t2 = 8 s + 10 s = 18 s
Con el desplazamiento total recién calculado aplicamos:
Δv = xtotal / ttotal
Δv = 152 m / 18 s
Δ v = 8.44 m/s
La velocidad media del automóvil Porsche en su viaje completo es 8.44 m/s
Problema 3
En el gráfico, se representa un movimiento rectilíneo uniforme de un carro por una carretera
|  |
a) Describe el movimiento del carro
b) calcula la distancia total recorrida por el carro.
c) ¿cuál fue el desplazamiento completo del carro?.
Solución
a) El gráfico del carro nos muestra que en t = 0 h, el carro poseía una velocidad de 16 km/h.
El carro en el primer intervalo de tiempo de 0 h a 0.4 h mantiene la misma velocidad de 16 km/h
El carro en el segundo intervalo de tiempo de 0.4 h a 0.8 h permanece en reposo (velocidad es 0 km/h).
El carro en el tercer intervalo regresa desde el tiempo de 0.8 h a 1.2 h mantiene la misma velocidad de - 16 km/h
b) para calcular la distancia total recorrida se encuentra el espacio recorrido en cada intervalo:
Datos:
Momento 1
|
Momento 2
|
Momento 3
|
|---|---|---|
| v1 = 16 km/h | v2 = 0 km/h | v1 = - 16 km/h |
| t1 = 0.4 h | t1 = 0.4 h | t1 = 0.4 h |
Como vamos a calcular la distancia del carro debemos tomar los valores numéricos de la velocidad positivos y nos queda utilizando la formula x = v.t:
Momento 1
|
Momento 2
|
Momento 3
|
|---|---|---|
| x1 = (v1).(t1) | x2 = (v2).(t2) | x3 = (v3).(t3) |
| x1 = (16 km/h). (0.4 h) | x2 = (0 km/h). (0.4 h) | x3 = (16 km/h). (0.4 h) |
| x1 = 6.4 km | x2 = 0 km | x3 = 6.4 km |
Nos queda que:
Xtotal = X1 + X2 + X3
= 16 Km + 0 km + 16 km
= 32 km
Xtotal = X1 + X2 + X3
= 16 Km + 0 km + 16 km
= 32 km
La distancia total recorrida por el carro es de 32 km. Recuerde que no consideramos el signo de la velocidad, por que, estamos hablando de distancia.
c) para calcular el desplazamiento del carro debemos tener en cuenta el carácter vectorial de la velocidad
Momento 1
|
Momento 2
|
Momento 3
|
|---|---|---|
| x1 = (v1).(t1) | x2 = (v2).(t2) | x3 = (v3).(t3) |
| x1 = (16 km/h). (0.4 h) | x2 = (0 km/h). (0.4 h) | x3 = (16 km/h). (0.4 h) |
| x1 = 6.4 km | x2 = 0 km | x3 = - 6.4 km |
Nos queda que:
Xtotal = X1 + X2 + X3
= 16 Km + 0 km - 16 km
= 0 km
Xtotal = X1 + X2 + X3
= 16 Km + 0 km - 16 km
= 0 km
El desplazamiento total del carro es de 0 km. Recuerde que en este problema podemos notar la diferencia entre la distancia y el desplazamiento.
Problema 4
En el gráfico, se representa un movimiento rectilíneo uniforme de un automóvil, averigüe gráfica y analíticamente la distancia recorrida en los primeros 4 s.
|  |
Solución
Datos
v = 4 m/s
|
Base = 4 s
|
t = 4 s
|
Altura = 4 m/s
|
De forma analítica utilizamos la formula de distancia
|
De forma gráfica utilizamos la formula de área de un rectángulo A =Base.Altura nos queda:
|
x = (4 m/s).(4 s)
|
A = (4 s).(4 m/s)
|
x = 16 m
|
A = 16 m
|
Analíticamente la distancia recorrida en los primeros 4 s es de 16 m
|
Gráficamente la distancia recorrida en los primeros 4 s es de 16 m
|
Problema 5
El Automóvil Bugatti Veyron de 2009 recorre una recta con velocidad constante. En los instantes t1 = 0 s y t2 = 6 s, sus posiciones son x1 = 10.5 cm y x2 = 35.5 cm. Determinar:
|  |
a) Velocidad del automóvil Bugatti Veryron.
b) La posición del autoBugatti Veryron en t3 = 2 s.
c) Las ecuaciones de movimiento del deportivo Bugatti Veryron.
Solución
Datos:
Momento 1
|
Momento 2
|
|---|---|
| x1 = 10.5 cm | x2 = 135.5 cm |
| t1 = 0 s | t2 = 6 s |
a) Como:
Δv = Δx/Δt
Δv = (x2 - x1) / (t2 - t1)
Δv = (35.5 cm - 10.5 cm) / (6 s - 0 s)
Δv = 25 cm / 6 s
Δv = 4.16 cm/s
Δv = (x2 - x1) / (t2 - t1)
Δv = (35.5 cm - 10.5 cm) / (6 s - 0 s)
Δv = 25 cm / 6 s
Δv = 4.16 cm/s
La velocidad de automóvil Bugatti Veyron es de 4.16 cm/s
b) Para t3 = 2 s:
Δx = Δv.Δt
Δx = (4.16 cm/s).(2 s)
Δx = 8.32 cm
Δx = (4.16 cm/s).(2 s)
Δx = 8.32 cm
El espacio recorrido del Bugatti Veyron después de iniciar su movimiento es 8.32 m. Recordemos que su posición inicial del punto de referencia era 10.5 m y como se desplazo 8.32m, entonces su posición después de transcurrir 2 s es de 18.82 m.
c) Para la ecuación del movimiento, tenemos en cuenta la formula General X = v.t + X0
Tomamos los datos que hemos obtenidos v = 4.16 cm/s, X0 = 10.5 cm, es decir; la ecuación es:
X = (4.16 cmm/s).t + 10.5 cm
ó sin las unidades nos quedad X = 4.16t + 10.5
ó sin las unidades nos quedad X = 4.16t + 10.5
Problema 6
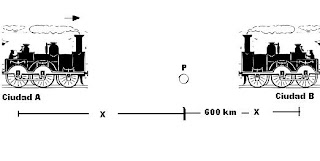
Dos trenes Metrópolis parten de dos Ciudades A y B, distan entre sí 600 km, con velocidad de 80 km/h y 100 km/h respectivamente, pero el tren de la ciudad A sale 2 horas antes. ¿Qué tiempo depués de haber salido el tren Metrópolis de la ciudad B y a qué distancia de la ciudad A se encuentran los dos trenes Metrópolis
|  |
Solución
El siguiente diagrama ayuda a ilustrar la situación presentada en el problema
|
Consideremos que los dos trenes Metrópolis se encuentran en el punto P de la trayectoria, por lo tanto el tren Metrópolis que parte de la ciudad A recorre un espacio X, mientras el tren Metrópolis que parte de la ciudad B recorre el espacio 600 km - X.
Llamamos t al tiemo que tarda el tren Metrópolis que parte de la ciudad B en llegar al punto P; por lo tanto el tiempo que tarda el tren Metrópolis de la ciudad A será t + 2h ya qué éste sale dos horas antes.
| Ciudad A | Ciudad B |
|---|---|
| vA = 80 Km/h | vB = 100 Km/h |
| X = vA(t + 2h) | 600 Km - X = vBt |
Aquí tenemos un sistema de dos ecuaciones con dos incógnitas "x" y "t", su solución se puede obtener por cualquiera de los métodos estudiados en matemática. Sumemos términos a término las ecuaciones (1) y (2):
| X = vA(t + 2h) | Ecuación (1) | |
| + | ||
| 600 Km - X = vBt | Ecuación (2) |
Al sumar nos queda X + 600 Km - X = vA(t + 2h) + vBt
600 Km = vA(t + 2h) + vBt
| 600 Km = 80 | Sustituyendo los datos |
| 600 Km = 80t | Realizando las multiplicaciones respectivas |
Al reducir terminos semejantes y transponer términos:
180t = 440 Km
= 440 Km
Donde t = 2.44 h
Al remplazar este valor en cualquiera de las ecuaciones tenemos:
X = 80 (t + 2h)
(t + 2h)
X = 80 (2.44h + 2h)
(2.44h + 2h)
X = 355.2 Km
El tiempo que tardan en encontrarse los dos trenes de Metrópolis después que sale el tren de la ciudad B es 2.44h
La que hay de la ciudad A a donde se encontraron los dos trenes de Metrópolis es de 355.2 Km
Problema 7
*****
Solución
| Ecuaciones del Movimiento MRU | Problemas de Aplicación del MRU |